题目描述
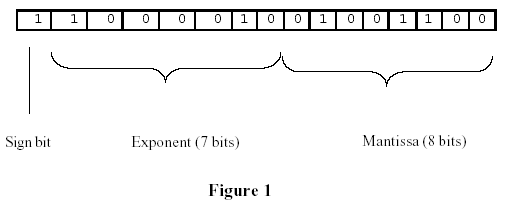
Floating point numbers are represented at the hardware level of most computer systems in normalized binary scientific notation. We will consider a hypothetical computer in which floating point numbers are represented in a 16-bit word. An example is shown in Figure 1. In the common Intel chips, the exponent of a float has 8 bits and the mantissa has 23 bits, otherwise the representation is the same as in Figure 1.

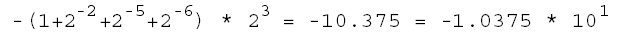


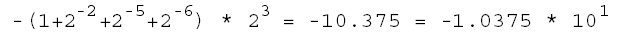
输入
The input contains an undetermined number of lines. Each line contains, starting in column 1, exactly 16 printable characters which can be any permutation of 0s and 1s. The first character represents the sign bit, the next seven characters, the exponent, and the last eight characters, the mantissa of a floating point number in normalized binary scientific notation according to the conventions discussed on the preceding page.
Each floating point number read from the input will be written by your program to the output file, one number per line.
输出
The following formatting conventions are required in your output:
The floating point numbers will be displayed in scientific notation (base ten).
Column 1 will either be blank (indicating a positive number or zero) or contain a minus sign (indicating a negative number).
Column 2 will contain a digit.
Column 3 will contain the decimal point.
Columns 4 - 9 will contain six additional significant digits of the floating point number.
The remaining columns will specify the exponent of scientific notation. The sign and magnitude of the exponent must of course be correct, but the exact format in which the exponent is displayed will be determined by the programming language you use.
样例输入 Copy
1100001001001100
0011111100000000
1011111110000000
0000000010101010
0011011111100000
1001111011100000
0101011001010101
0100011011101101
0111111111111111
1100001000101100
0000000000000000
1000000000000000
样例输出 Copy
Program 6 by team X
-1.037500e+001
1.000000e+000
-1.500000e+000
1.804180e-019
7.324219e-003
-2.182787e-010
1.117389e+007
2.465000e+002
3.682143e+019
-9.375000e+000
0.000000e+000
0.000000e+000
End of program 6 by team X