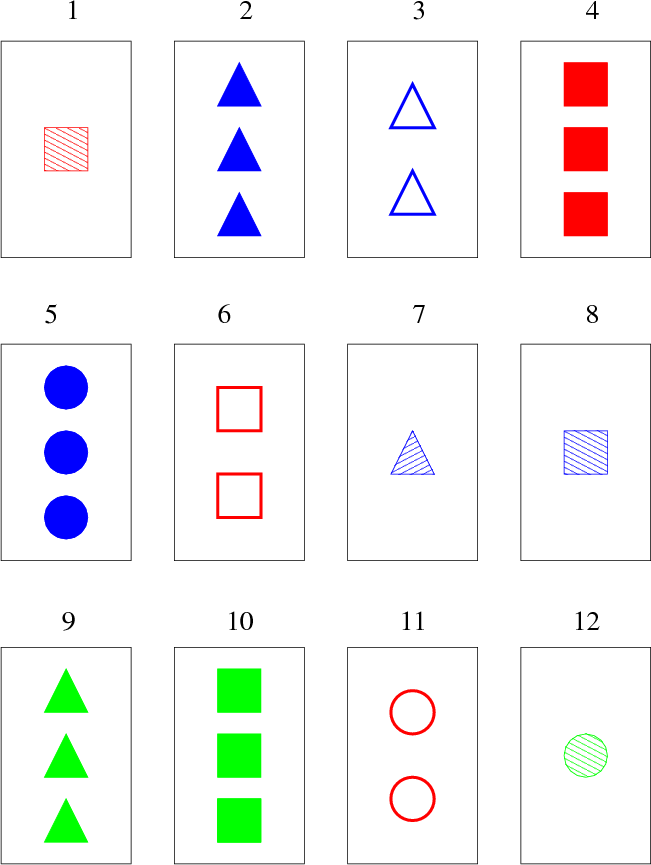
The game of Sets is a very popular card game ( http://en.wikipedia.org/wiki/Set_(game)). The game is played with a special deck of cards, where each card has a unique picture on it. This is an example of such a card:
Each of the cards is uniquely identified by its four properties: the shape shown in the picture (square, triangle, circle), the count of these shapes (one, two, three), their color (red, green, blue), and the fill style (empty, striped or full). For each combination of values there is exactly one such card in the deck. Thus the total number of cards in the deck of the original game is 34 = 81. The main concept of this card game is a Set. A Set consists of three cards such that for each property, they are either all the same, or all are different. In other words, three cards are not a Set if and only if you can say “Two of them are … and one is not.” In the picture below, the cards 1, 4, and 6 form a Set: they are all red, all are squares, the counts are different, and so are the fill types. The cards 2, 3, and 9 do not form a Set, for example because two of them are blue and one is not.
Problem specification In this problem we will play a more general version of the game. There will be N card properties, and for each of these properties there will be M different values it can obtain. The deck will contain exactly one card for each possible combination of properties. Thus there will be MN cards in the deck. In this more general game, a Set consists of exactly M cards such that for each of the N properties the following holds: Either all the cards have the same value of this property, or all of them have different values. You will be given the values N, M, a positive integer K, and a description of K different cards from the deck. Your task is to find the number of different Sets that can be created from the given cards. (Note that some of those Sets may overlap.)

The first line of the input file contains an integer T specifying the number of test cases. Each test case is preceded by a blank line. Each test case looks as follows: The first line contains three positive integer N, M and K giving the number of different properties of the cards, the number of different values of a single property, and the number of cards drawn. Each of the next K lines describes one of these cards. The i-th of these lines (1 ≤ i ≤ K) contains exactly N numbers pi,j (1 ≤ j ≤ N), 1 ≤ pi,j ≤ M. Value pi,j is the value of the j-th property of the i-the card.

For each test case output a single line with a single integer – the number of different Sets that can be made from the given cards.

This example input corresponds to the image in the problem statement. The four properties are described in this order: shape (square, triangle, circle), count (one, two, three pieces), color (red, green, blue) and fill style (empty, striped, full). These are the 11 different sets: (1,4,6), (1,7,12), (2,3,7), (2,6,12), (3,4,12), (3,5,8), (4,5,9), (5,11,12), (6,8,10), (7,10,11), and (8,9,11).

IPSC 2008