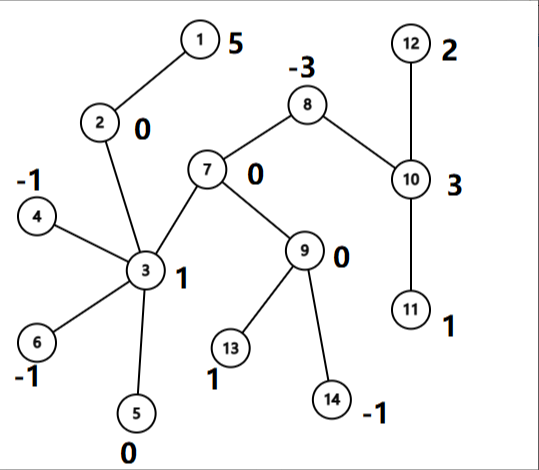
题目描述
给定一棵树,其包含 n 个结点和 n − 1 条边,每条边连接两个结点,且任意两个结点间有且仅有一条简单路径互相可达。
每次操作可以断一条边,随后选择分裂出的两棵树中的一棵树删除,请最小化操作次数使得最后剩下的树的点权和最大。
每次操作可以断一条边,随后选择分裂出的两棵树中的一棵树删除,请最小化操作次数使得最后剩下的树的点权和最大。
输入
第一行包含一个数 n (1<=n<=4*10^5) ,代表树中点的个数。
第二行包含 n 个整数 ai (-10^9<=ai<=10^9) ,代表点 i 的点权。
随后 n-1 行,每行两个整数 u,v (1<=u,v<=n,u!=v) ,代表树的边。
第二行包含 n 个整数 ai (-10^9<=ai<=10^9) ,代表点 i 的点权。
随后 n-1 行,每行两个整数 u,v (1<=u,v<=n,u!=v) ,代表树的边。
输出
输出两个整数,分别代表最后剩下的树的点权和以及对应的最小操作次数。
样例输入 Copy
14
5 0 1 -1 0 -1 0 -3 0 3 1 2 1 -1
1 2
2 3
3 4
3 5
3 6
3 7
7 8
7 9
8 10
10 11
10 12
9 13
9 14
样例输出 Copy
10 3
提示