题目描述
给定一棵根为 1 的树,其包含 n 个结点和 n − 1 条边,每条边连接两个结点,且任意两个结点间有且仅有一条简单路径互相可达。在这里,我们认为当 n=1 时,根节点也是叶节点。
我们定义一个子节点都是叶节点且子树都被打上标记的节点为 “枝” ,被标记的叶节点都是 “花” 。在任何时刻你都可以选择一个 “枝” ,把它的所有子节点,也即 “花” 折下来。操作过后,会删除选定的 “枝” 和它的 “花” 间的连边, 选定的 “枝” 会变成新的 “花” 。
在每个时间点你都可以选取一个没有被标记过的节点来打上标记,最开始没有节点被标记。
你的目标是将树变为一枝 “花” 并最小化任何时间点树上被标记点数量的最大值。
我们定义一个子节点都是叶节点且子树都被打上标记的节点为 “枝” ,被标记的叶节点都是 “花” 。在任何时刻你都可以选择一个 “枝” ,把它的所有子节点,也即 “花” 折下来。操作过后,会删除选定的 “枝” 和它的 “花” 间的连边, 选定的 “枝” 会变成新的 “花” 。
在每个时间点你都可以选取一个没有被标记过的节点来打上标记,最开始没有节点被标记。
你的目标是将树变为一枝 “花” 并最小化任何时间点树上被标记点数量的最大值。
输入
第一行包含一个数 n (1<=n<=4*10^5) ,代表树中点的个数。
随后 n-1 行,每行两个整数 u,v (1<=u,v<=n,u!=v) ,代表树的边。
随后 n-1 行,每行两个整数 u,v (1<=u,v<=n,u!=v) ,代表树的边。
输出
输出一个整数,代表任何时间点树上被标记点数量的最大值的最小值。
样例输入 Copy
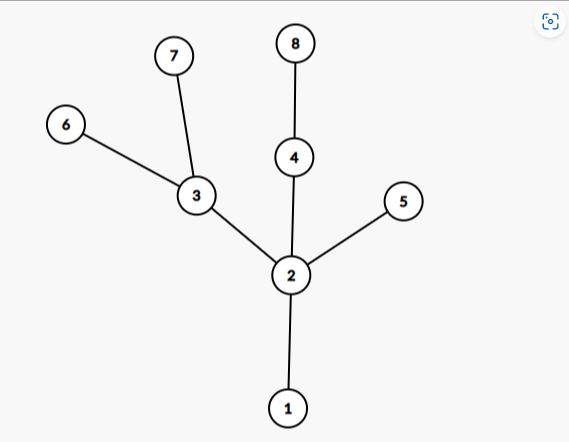
8
1 2
2 3
2 4
2 5
3 6
3 7
4 8
样例输出 Copy
4
提示